Digital sampling of analog signals can produce surprising effects. It is tricky to explain and understand the frequency aliasing, which happens when undersampling. What is the aliased frequency? Why are there positive and negative frequencies in FFT, but only one Nyquist frequency?
One good way to visualise this is to think about the old movies. Remember how the wheels used to turn back? It is the so-called Wagon-wheel effect, which is basically frequency aliasing. Assuming the movie runs with fs = 16 Hz sampling frequency, the wheel diameter was d = 50 cm we reach the Nyquist frequency at v = pi * d * fs * 0.5 = 45 km/h. At this speed we cannot see anymore if the wheels are moving forward or backward. Beyond it our brain takes a shortcut and thinks the wheel is turning back - a negative frequency, which will go up again with the growing speed, until at 90 km/h the movement will stop. It is frequency aliasing to 0 or DC aka stroboscopic effect.
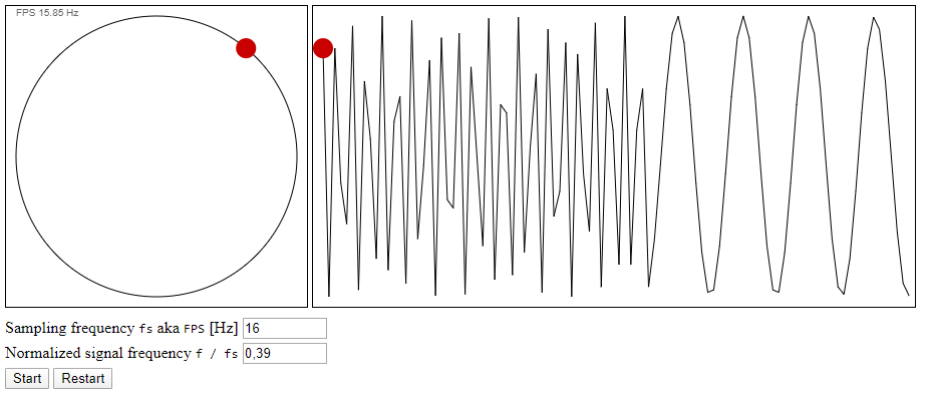
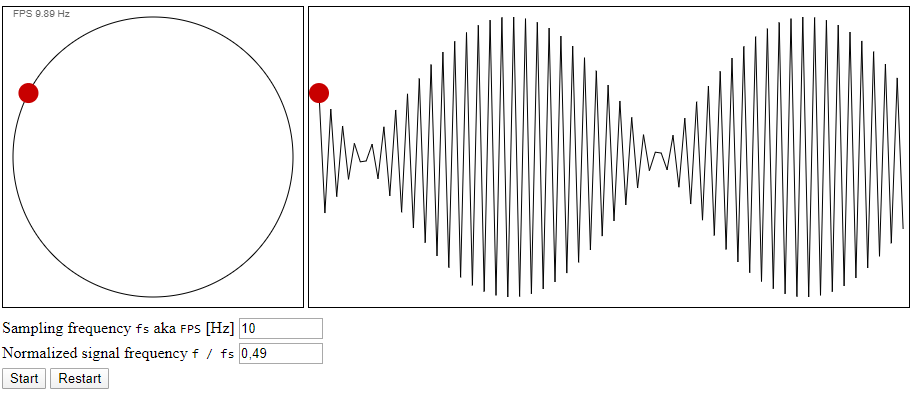
I created a small simulation in HTML5 / JavaScript to visualise this effect. On the left there is a turning wheel, which is sampled at the defined frequency fs aka FPS for Frames Per Second in Y axis. The rotating frequency is normalised by sampling frequency to allow synchronised manipulation, also during simulation (use arrow keys). The mathematically positive direction is to the left or counterclockwise.
There are a few interesting effects, some psycho-optical:
- at Nyquist frequencies
f / fs = 0.5 + kwhere k - integer the amplitude may change arbitrarily with the phase, including zero - close to the Nyquist frequency, say
f / fs = 0.49we have amplitude modulation ('beat frequency') - at DC frequencies
f / fs = kthe amplitude is constant, including zero - when I set the wheel frequency to 0.3, the wheel appears to turn to the right at
fs = 16 Hzand to the left atfs = 10 Hz. YMMW. The sampled signal doesn't look like sine any more. - at
f / fs = 0.33333the wheel seems to turn to the left even at high FPS
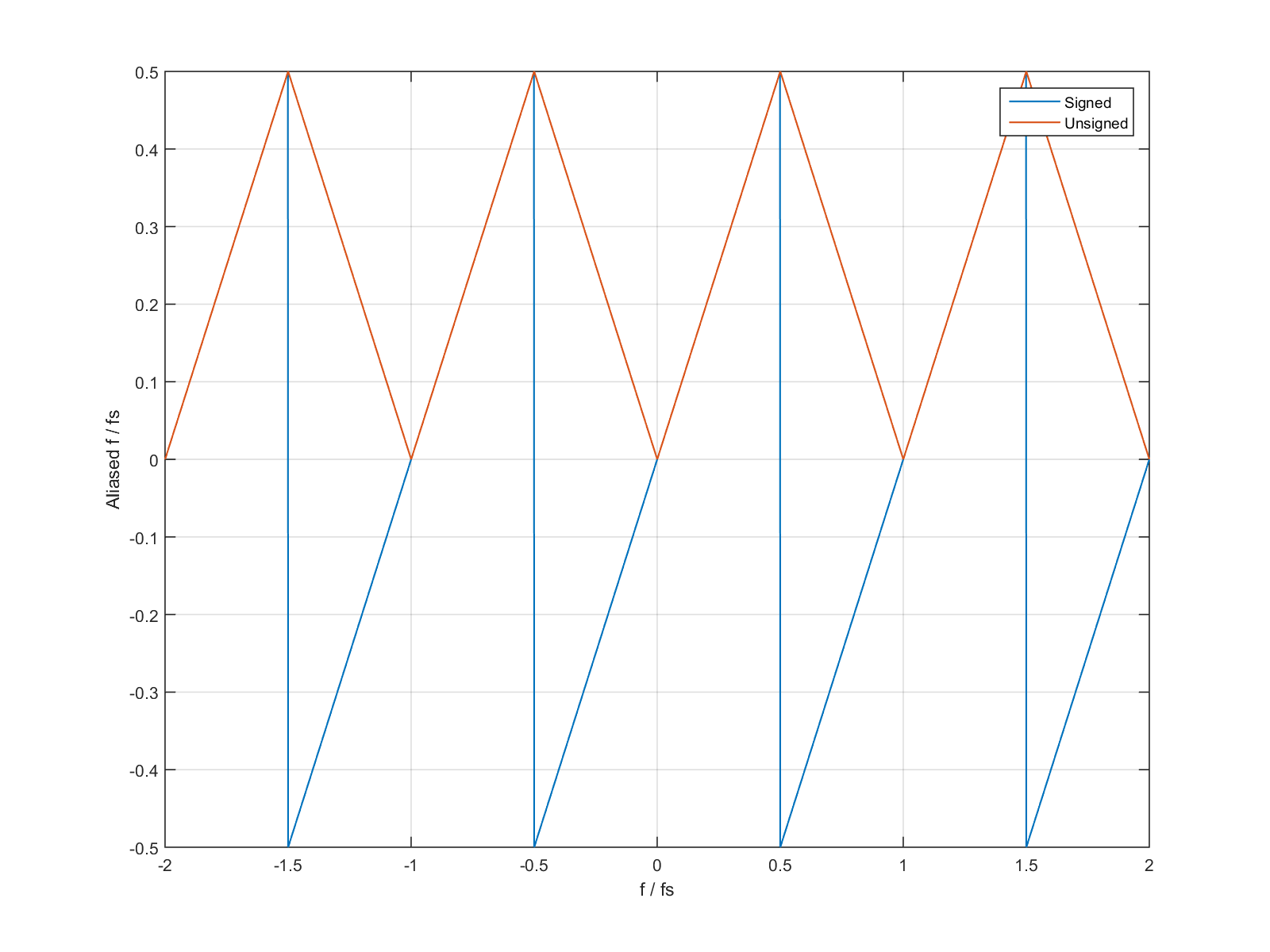
The signed aliased frequency fa can be calculated in Matlab like fa = (mod(f / fs + 0.5, 1) - 0.5) * fs, where mod(x, 1) >= 0. But very often we are interested in unsigned frequency. Frequency sign changes only phase shift or amplitude sign. And the frequency is just fu = abs(fa). In FFT there is one DC and one Nyquist amplitude. For real signals the negative frequencies are redundant.
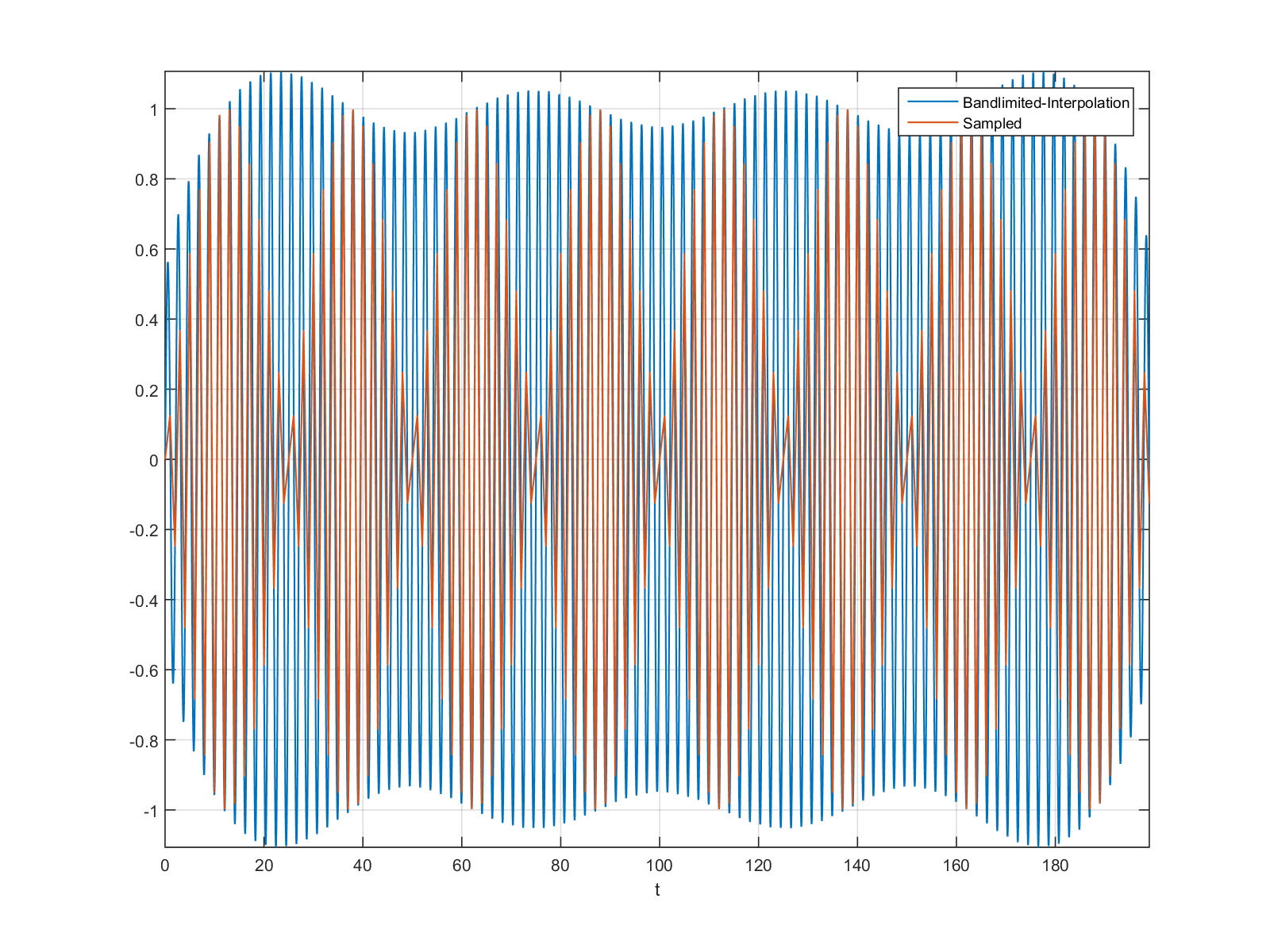
Even if the result doesn't look like a sine to our eyes, the Shannon-Nyquist theory can recover the underlying signal using bandlimited interpolation via xr = sinc(Tr - Ts) * xs, where Ts, xs - original sampling, Tr, xr - bandlimited upsampling and matrix multiplication. See e.g. Smith, J.O. Digital Audio Resampling Home Page http://www-ccrma.stanford.edu/~jos/resample/, [2018]).. Here once again an almost-Nyquist example of f / fs = 0.49, upsampled by 10. Bandlimited interpolation is basically a set of long FIR filters, which makes it often unpractical for real resampling work. The artefacts (amplitude should be 1.0) are due to the truncation.
Aliasing is also a cool tool for downsampling, like in Software Defined Radio (SDR). Mostly quadrature sampling is used, so we get both X and Y axis and signed frequency. You just do not want to cross the Nyquist frequency.